Code: Word2Vec in Spark

Here is a snippet that might be useful to you if you are looking to implement Word2Vec and save the embeddings of the trained model. I’ve added types to the variables as well as to some placeholder names to make it easier to understand what is expected as an input to various functions

First you will need to import Word2Vec and Word2VecModel

    import org.apache.spark.ml.feature.{Word2Vec, Word2VecModel}

Then you will need to import spark session’s implicits as you will be working with Datasets.

    import sparkSession.implicits._

Then you need to prepare your input data for the algorithm. The training algorithm expects a Dataset of Sequences of Strings. In the example below “getTrainset” is a function that retrieves your training corpus and formats it into the required type.

    val trainset: Dataset[Seq[String]] = getTrainset() 

Now you are ready to start using Word2Vec. You need to first configure the Word2Vec algorithm with the parameters that you have selected.

    val wordToVec: Word2Vec = new Word2Vec()
    .setInputCol("column-name-of-your-trainset-dataset")
    .setOutputCol("output-column-name")
    .setStepSize(learningRateFloat)
    .setVectorSize(vectorSizeInt)
    .setWindowSize(windowSizeInt)
    .setMaxIter(numberOfIterationsInt)
    .setMinCount(minimumCountForDiscartingInt)
    .setNumPartitions(wordToVecPartitions)

Next comes the training step.

    val model = wordToVec.fit(trainset)

Once your model has been trained you will want to process it and save it in the format that you want. Because you are dealing with a dataset you need to map the results to something more type safe. You can do this with a case class as follows:

    case class MyCustomType(word: String, vector: Vector) {
        def toPair = (word.toLong, vector.toArray)
    }

    model.getVectors.as[MyCustomType].map(_.toPair)

Lastly, you want to save you model. Note that the Word2Vec model does have a save function that saves it in a special format easily reloadable into a Word2VecModel. In this example we will save to parquet instead as you may need a more raw version of your model.

   model
      .repartition(partitionsToSaveModelInto)
      .withColumnRenamed("_1", "word")
      .withColumnRenamed("_2", "vector")
      .select("word", "vector")
      .write.parquet(options.outputFile)

Spark Word2Vec: lessons learned

This post summarises some of the lessons learned while working with Spark’s Word2Vec implementation. You may also be interested in the previous post “Problems encountered with Spark ml Wod2Vec”

Lesson 1: Spark’s Word2Vec getVectors returns the  unique embeddings

As mentioned in part 2, the transform function aims to return the vectors for words within the given sentences. If you want the actual trained model, and therefore the unique word to vector representations you should use the getVectors function

Lesson 2: More partitions == more speed == less quality

There is a balance that you need to determine between having a fast implementation vs one with good quality. Having more Word2Vec partitions means that the data is separated into many smaller buckets, losing context of the words in other buckets. The data is only brought together at the end of an iteration. For this reason, you don’t want to split your data into too many partitions. However, you also don’t want to lose out on parallelism – after all you are using spark because you want distributed computation. Play around with the total partitions – the right value for this parameter will differ depending on the problem. Also remember that less partitions means less parallelism and therefore a slower algorithm.

Lesson 3: More iterations == less speed == more quality

As mentioned in lesson 2, the data from various partitions is brought together at the end of each iteration. Having more iterations means more context from the different buckets and more time training. This means that more iterations can lead to better results, but they do have an impact on the running time of the algorithm.

Lesson 4: Machine learning algorithms need a lot of hardware

This probably doesn’t come as a surprise, but it is still worth mentioning. You are using a machine learning algorithm on a distributed cluster and you keep having to give 1 thing more memory, namely your driver.

Lesson 5: Save things to parquet

Why? efficient data compression built for handling bulk data leads to less memory issues.

Lesson 6: Spark ml Word2Vec is not mockable

If you are writing tests for your Spark jobs, which you should be doing, you will probably try to mock out Spark’s Word2Vec implementation as it is nondeterministic. You will soon be greeted by an error message stating that Word2Vec cannot be mocked. You will then quickly find out that this is a final class in the ml library. To get around this you can wrap your call to Word2Vec in a function and inject it into the function that you are testing.

Problems encountered with Spark ml Word2Vec

This post aims to summarise some of the problems experienced when trying to use Spark’s ml Word2Vec implementation.

Out of memory exception

Spark’s Word2Vec implementation requires quite a bit of memory depending on the amount of data that you are dealing with. This is because the driver ends up having to do a lot of work. You may experience this problem with various machine learning implementations in Spark.

All you have to do is increase the total memory allocated to your driver using spark-submit’s option driver-memory. Note that your cluster may have an upper limit set which you might need to increase. The error message that you get if you set the driver memory to a value above this threshold is  very straight forward. It pretty much tells you to increase the limit by changing the value of the cluster’s yarn.scheduler.maximum-allocation-mb.

In my case, the driver was using 30 GB, so I gave it 40 GB.

Total size of serialized results of X tasks (Y MB) is bigger than spark.driver.maxResultSize (Y MB)

The Word2Vec algorithm needs to deal with result sizes larger than your normal cleaning job. You can increase Spark’s limit by increasing the value of spark.driver.maxResultSize.

Default column name not found

Spark’s ml Word2Vec implementation deals with Dataframes. This means that it relies on string names of columns rather than concrete types. You are getting this error because the Dataframe’s column name does not match the default name expected by the Word2Vec training function.  There are 2 options to fix this:

1. Change the name expected by Word2Vec to the name of your input Dataframe’s column using the setInputCol function of Word2Vec. If you have not set a column name, then it is probably value.
2. Change your input Dataframe’s column name to that expected by Word2Vec. The name expected by Word2Vec is inputCol.

OutOfMemoryError: GC overhead limit exceeded

As the driver is doing a lot of work, the default Garbage Collector seems to struggle to catch up with the cleanup. To fix this you can use concurrent garbage collection by enabling it through the Java Options. You can do this by adding XX:+UseConcMarkSweepGC to the Java options in your spark-submit.

Cannot resolve ‘`X`’ given input columns: [value, w2v_993c88fe4732__output]

As you are dealing with Dataframes when managing the results of Word2Vec you are probably trying to map these to your custom datatype after retrieval. You get an error like this if your custom type’s constructor expects the wrong parameters. As you may be retrieving the vectors in two different ways let’s look at the expectations of each one:

• Using dataframe returned by transform: this expects a type that takes in two parameters -> value: Array[String], vector: Vector
• Using dataframe returned by getVectors -> this expects a type that takes in two parameters: word: String, vector: Vector

Ensure that when you use <dataframe>.as[<customType>] that the custom type expects the above-mentioned parameter types.

Duplicates in output from Word2Vec

When saving your model you may notice that you are getting duplicated words with different vectors in your word-vector representation. One words should have one vector representation. This may be especially confusing if you re moving from Google’s implementation to Spark’s. This is happening because you are using the transform function. This function takes in the sentences that you trained the model with and returns a word-vector representation for each word in the given set. This means that repeated words across different sentences will also appear in your result with the vector representations most appropriate for their context at that point. If what you want is the single vector representation of a word, you should get the correct embeddings by using the getVectors function.

Failed to register classes with Kryo

This is not specific to Word2Vec but it did happen during the implementation. This generally means that your manual Kryo serialization registration, which is done for optimization reasons, is missing a type. Find out the type that you are missing and register it using kryo.register(classOf[<myClass>]).

Memory issues when saving the results of getVectors

Once you are almost done and all you need to do is just save your trained Word2Vec embeddings for future use you might be greeted by some memory issues. If you are, you are probably trying to either save the whole model into a single file or you are saving it into partitioned plain text files on HDFS. You have a coupe of options here.

Word2VecModel has a function save which allows you to save the model in a format that can be re-loaded into a Word2VecModel using the load function. This wasn’t quite what I needed in my case, but it may be appropriate for your use case.

I needed to save the embeddings as normal text in order for another spark job to consume it as input to a second machine learning algorithm.  For this reason, I went for my second file-saving option: saving to parquet. This can be done with the following code snippet:

model
.repartition(partitions)
.withColumnRenamed("_1", "word")
.withColumnRenamed("_1", "vector")
.select("word", "vector")
.write.parquet("some output path")

An overview of Word2Vec

Word2Vec (W2V) is an algorithm that takes in a text corpus and outputs a vector representation for each word, as depicted in the image below:

There are two algorithms that can generate word to vector representations, namely Continuous Bag-of-words and Continuous Skip-gram models.

In the Continuous Bag-of-words model the task of the neural network is to predict a word given the context its context. In the Skip-gram model the task of the neural network is the opposite: to predict the context given the word. 

This post will focus on the Skip-gram model. For more information on the continuous bag of words check out this article.

The literature describes the algorithm in two main ways. The first being as a neural network and the second as a matrix factorisation problem.  This post will follow the neural network based description.

If you are familiar with neural networks already, you can think of Word2Vec as a neural network where the input is a word and the output is a probability of that word forming part of a particular context. The resulting vectors for each word are then the weights leading from  the word’s input node towards the hidden layer.

The Skip-gram model takes in a corpus of text and creates a hot-vector for each word. A hot vector is a vector representation of a word where the vector is the size of the vocabulary (total unique words). All dimensions are set to 0 except the dimension representing the word that is used as an input at that point in time. Here is an example of a hot vector:

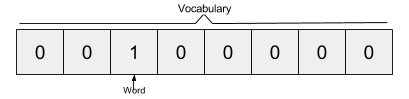
The above input is given to a neural network with a single hidden layer which looks as follows:

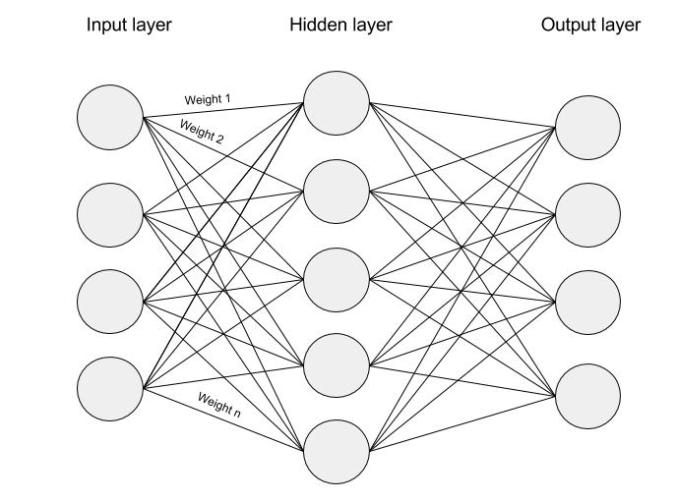
Each dimension of the input passes through each node of the hidden layer. The dimension is multiplied by the weight leading it to the hidden layer. Because the input is a hot vector, only one of the input nodes will have a non-zero value (namely the value of 1). This means that for a particular word only the weights associated with the input node with value 1 will be activated, as shown in the image below:

As the input in this case is a hot vector, only one of the input nodes will have a non-zero value. This means that only the weights connected to that input node will be activated in the hidden nodes. An example of the weights that will be taken into account is depicted below for the second word in the vocabulary:

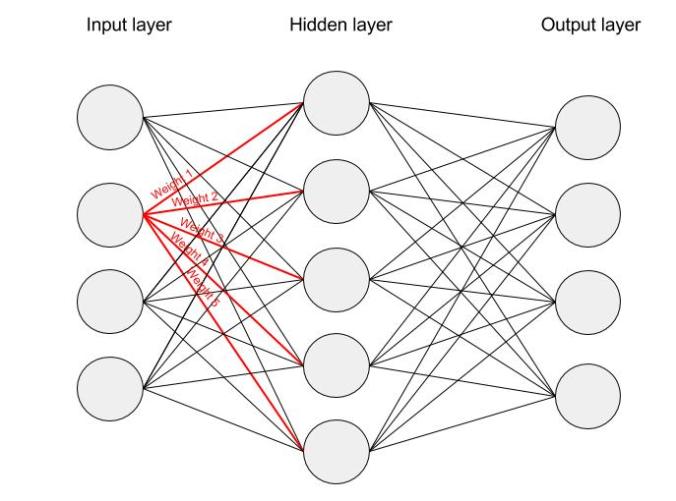
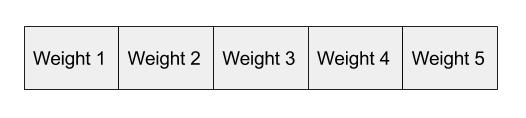
The vector representation of the second word in the vocabulary (shown in the neural network above) will look as follows, once activated in the hidden layer:

Those weights start off as random values. The network is then trained in order to adjust the weights to represent the input words. This is where the output layer becomes important. Now that we are in the hidden layer with a vector representation of the word we need a way to determine how well we have predicted that a word will fit in a particular context. The context of the word is a set of words within a window around it, as shown below:

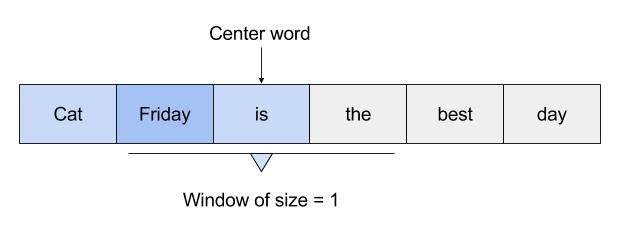
The above image shows that the context for Friday includes words like “cat” and “is”. The aim of the neural network is to predict that “Friday” falls within this context.

We activate the output layer by multiplying the vector that we passed through the hidden layer (which was the input hot vector * weights entering hidden node) with a vector representation of the context word (which is the hot vector for the context word * weights entering the output node).  The state of the output layer for the first context word can be visualised below:

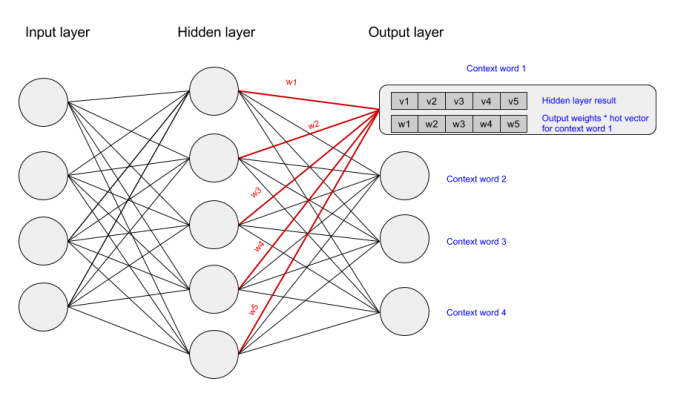
The above multiplication is done for each word to context word pair. We then calculate the probability that a word belongs with a set of context words using the values resulting from the hidden and output layers. Lastly, we apply stochastic gradient descent to change the values of the weights in order to get a more desirable value for the probability calculated.

In gradient descent we need to calculate the gradient of the function being optimised at the point representing the weight that we are changing. The gradient is then used to choose the direction in which to make a step to move towards the local optimum, as shown in the minimisation example below.

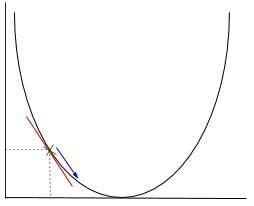
The weight will be changed by making a step in the direction of the optimal point (in the above example, the lowest point in the graph). The new value is calculated by subtracting from the current weight value the derived function at the point of the weight scaled by the learning rate.

The next step is using Backpropagation, to adjust the weights between multiple layers. The error that is computed at the end of the output layer is passed back from the output layer to the hidden layer by applying the Chain Rule. Gradient descent is used to update the weights between these two layers. The error is then adjusted at each layer and sent back further. Here is a diagram to represent backpropagation:

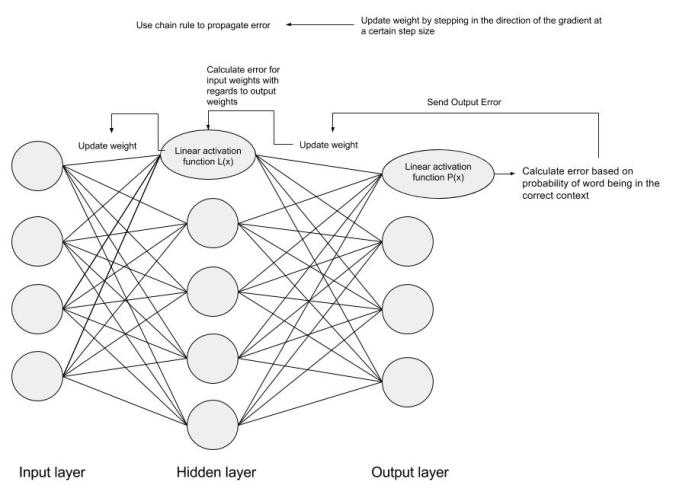
I’m not going to go into the details of Backpropagation or gradient descent in this post. There are many great resources out there explaining the two. If you are interested in the details of these, Standford University tends to have great freely available lectures and resources on Machine learning topics.

The final vector representation of the word will be the weights (after training) that connect the input node for the word to the hidden layer. The weights connecting the hidden and output layers are representations of the context words. However, each context word is also in the vocabulary and therefore has an input representation. For this reason, the vector representation of a word is only that of the input vectors.

Small comparison of Google Word2Vec vs Spark Word2Vec

Word2Vec (W2V) is an algorithm that takes in a text corpus and outputs a vector representation for each word. You can read more about it in my previous blog post.

There are various implementations of Word2Vec out there ready for you to use. Some of these include:

• Google’s first implementation
• Spark’s mlib and ml implementations
• TensorFlow’s implementation
• Gensim implementation
• PiPy implementation

This post aims to only briefly compare the first two, namely Google’s first implementation and Spark’s ml implementation. This is mainly useful for you if:

• You are considering whether to move from Google’s first implementation to Spark’s one
• You are considering whether to use either of these

 

The following table summarises the differences between these:

Attribute	Google implementation	Spark implementation (ml)
Architecture	Skip Gram	Skip gram
	Continuous bag of words
Training algorithm	Hierarchical softmax	Hierarchical softmax
	Negative sampling
Notes	Highly optimized, but not distributed.	Depending on the parameters and the data, large speed gains can be noticed. I’ve seen it getting 60% speed up with minimal change to results.
Mainteinability	No longer maintained	Still maintained and supported by spark
Including in your project	Requires you to download the source code directly and save it into your project	The library comes with Spark already
Failure management	A failure will crash the process	A failure will cause Spark to try a second attempt. This is great for intermittent cases such as network connections being lost.
Stability	Stable	Possible instabilities that emerge from moving to a distributed model. In other words – possible standard Spark problems.
Optimizable parameters	Parameter name
Vector size	size	setVectorSize
Learning rate	alpha	setStepSize
Input file	train	Pass your data frame
Output file	output	Save using Spark
Window size	window	setWindowSize
Use hierarchical softmax	hs	No other option, this is the default
Distribute into x parallel processes	threads	setNumPartitions
Total iterations	iter	setMaxIter
Minimum occurrences of a word to be considered	min-count	setMinCount